Цитата:
Сообщение от Алексей
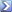
Как читается выражение ([vn]ω + [ωn]v)?
|
Это выражение читается: векторное произведение вектора v на вектор n и умноженное на скаляр ω складывается с векторным произведением векторов ω и n, умноженым на скаляр v. Ещё раз повторяю, квадратными скобками обозначается векторное произведение
векторов, скаляр не должен оказываться в нутри квадратных скобок.
И единичный вектор n, в твоём употреблении - это совсем ненужный костыль, который тем более работает только с центробежной силой кориолиса, выдовая совершенно неверные результаты, если линейная скорость движущегося по кругу тела направлена не по касательной к окружности, на которой оно расположено, проще говоря, если тело изменяет радиус своего движения по кругу.
Цитата:
Сообщение от Vladimir2
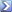
Компромис найден, идём дальше. Преобразуем эту формулу для нашего случая:
v = u; ωR = v;
Тогда имеем:
Fк = m/R ([uωR] - [ωRu]) = m/R ([uv] - [vu])
Как видим сила Кориолиса делится на две равных части, каждая из которых перпендикулярна своей оси вращения.
|
Вот здесь дальше есть путанница, что есть что. Вернёмся к нашим обозначениям:
0. На сколько я понял, у нас установилось негласное правило выделять вектора жирным шрифтом, скаляры простым.
1.
v - это линейная скорость тора.
2.
u - это скорость жидкости, по отношению к тору (а точнее в СО тора).
3.
ω - это угловая скорость тора.
4.
R - это радиус-вектор тора. Векторное умножение [
ωR] даёт вектор скорости тора
v.
По сему, если переписать формулу правильно, с учётом этих разъяснений и
изначальной формулы силы Кориолиса, то:
Fк = 2m[
uω] = m([
uω] - [
ωu]) = m/
R ([
u[
ωR]] - [[
ωR]
u]) = m/
R ([
uv] - [
vu]) = ... что в итоге равно ... = 0, ибо вектора u и v параллельны и их векторное произведение даёт 0.
И интересно существует-ли операция деления скаляра на вектор

Подозреваю, введение вектора R в формулу ошибочно, надо потом будет подумать над этим ещё.
Ваши мысли?